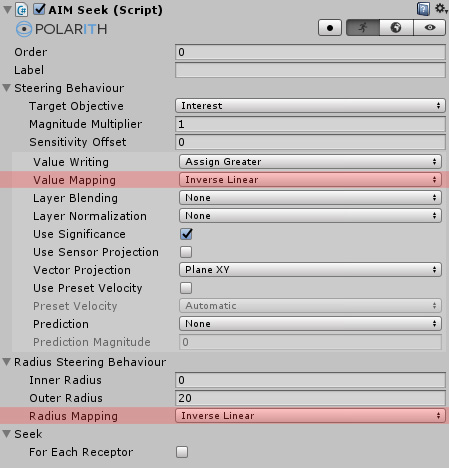
A MappingType is a concept mainly but not exclusively utilized by radius steering behaviours (e.g. Seek). The magnitude generated by such a behaviour is depended on the proximity to perceived objects. For example, given a behaviour having an OuterRadius of 100 and two objects with a distance of 50 and 75. With the default MappingType inverse linear, the resulting magnitudes are 0.5 and 0.25. This example shows why you most likely want to use inverse mapping, because you often want the objects further away to have a lower impact on your agents. In general, input values are mapped within a range of [0, 1]. Given the above-mentioned example, here are the results for the seven different mapping types.

Mapping type	Result 25	Result 50	Result 75
Constant	1	1	1
Linear	0.25	0.5	0.75
Inverse Linear	0.75	0.5	0.25
Quadratic	0.0625	0.25	0.5625
Inverse Quadratic	0.9375	0.75	0.4375
Square Root	0.5	0.707	0.866
Inverse Square Root	0.5	0.293	0.134

Besides the radius mechanism, mapping types are also very important for the writing of objective values (value mapping) to influence how magnitudes are written for matching receptor directions.

By using the MappingType, it is possible to adapt behaviours to different situations. For example, a Seek which samples obstacles might benefit from an inverse quadratic mapping. This way, an obstacle becomes more important to an agent much faster depending on how close it is to the agent. To achieve the opposite effect, let's have a closer look at the inverse square root mapping. This type would result in an agent which reacts to an obstacle very lately. Imagine two agents which play the Chicken game. The agent with the inverse square root mapping would win over an agent with another mapping type under the assumption that both have the same OuterRadius. Figure 1 below illustrated how the different mapping types work.

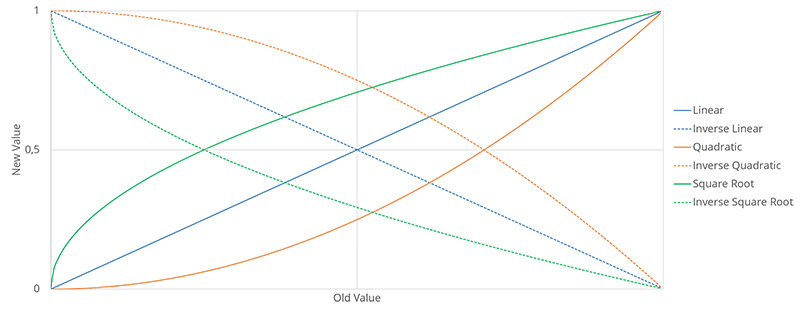
Figure 1: Shows the resulting graph plots for the six different mapping types.